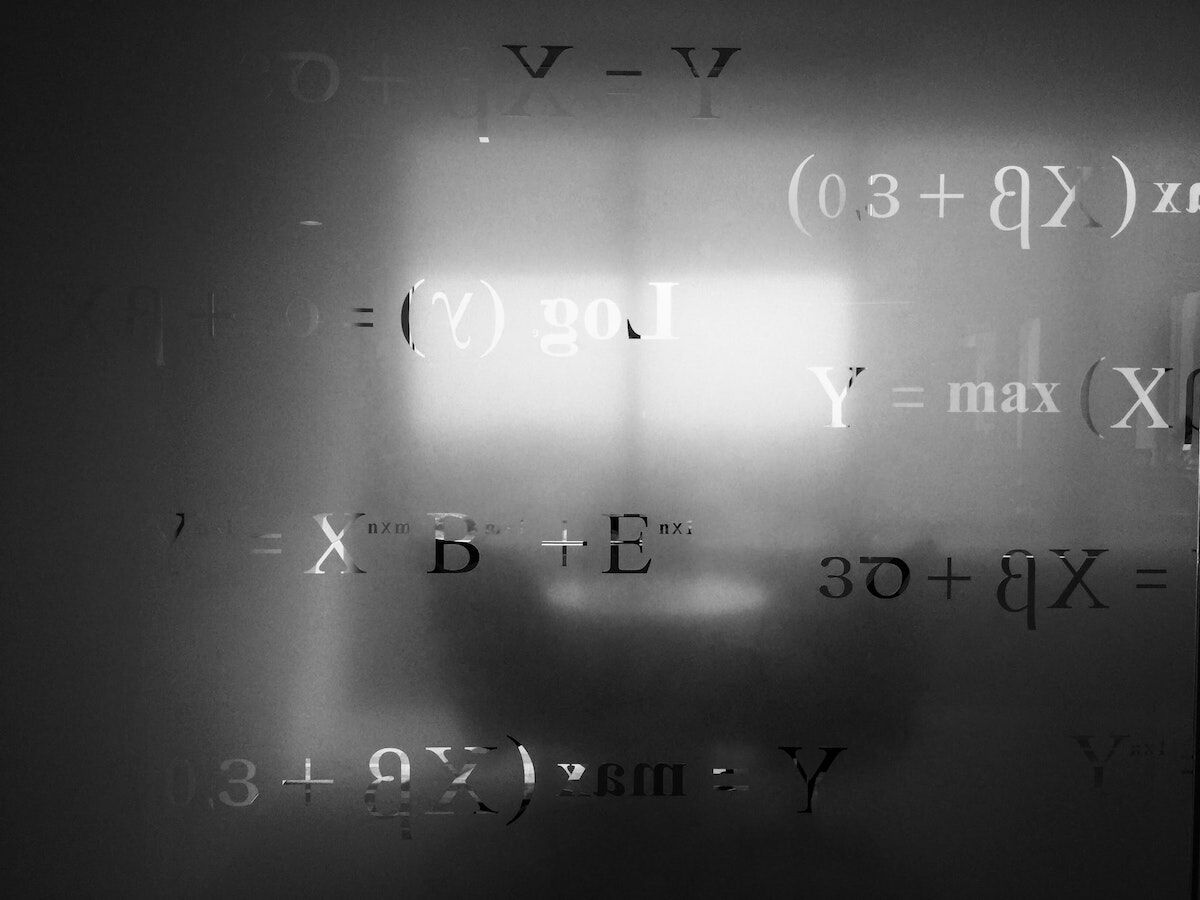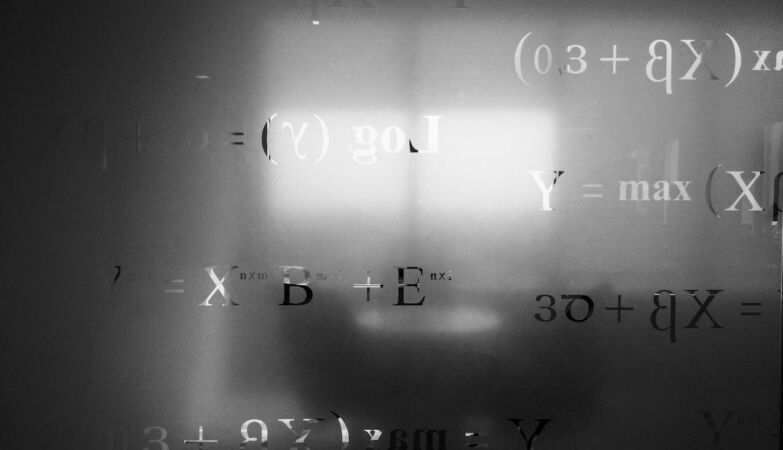
Two groups of mathematicians have just widen the mastery of mathematical incognibility through Hilbert’s famous 10th problem.
Em 1900, David Hilbert presented 23 fundamental problems for mathematics, dreaming of a complete system where all mathematical truths were proven true or false.
However, in the 1930s, Kurt Gödel demonstrated that such an idea was impossible, proving that Any mathematical system would contain indecidable statements.
Alan Turing He then reinforced this idea by showing that there are problems impossible to solve, even with computational algorithms.
Among the problems of Hilbert, the 10.º sought to know if there would be an algorithm capable of determine if a diofantine equation has entire solutions. Diophantin equations are precisely polynomic equations in which the solutions sought are integers.
Em 1970, Yuri Matiyasevich proved that such a algorithm does not existmaking this problem equally undecidable.
For decades, mathematicians have tried to extend the indecidability of Hilbert’s 10th problem to other structures, such as algebraic integers.
The approach used was based on the correspondence between diophantin equations and the problem of turing. However, as a grade A, this correspondence was crumbled when the solutions allowed non-integer numbers.
In the 2000s, Sasha Shlapentokh And other mathematicians developed strategies to circumvent this difficulty, adding terms to the diophantin equations that forced solutions to behave as whole.
However, a case persisted: the rings containing the imaginary number.
The key to solving this case lived in special elliptical curves that should meet complex conditions. However, building these curves was an extremely difficult problem.
Until…
At the beginning of December, Peter Koymans and Carlo Paganoexperts in elliptical curves, resolved this more recent challenge.
In a study in arXivThe mathematicians managed to create an elliptical curve that preserved the structure of solutions in the different algebraic rings.
This discovery allowed them to demonstrate that Hilbert’s 10th problem remains undeniable for all integer rings.
Last Thursday, an independent team confirmed, through another study in the arXivthe result of Koymans and Pagano. In this case, they were under investigation Another type of equations.
Both groups of investigators have agreed that both methods can be combined to advance related problems.
“There is a possibility that the two methods can be used together to do even more,” he praised Manjul BhargavaMathematician at Princeton University, who was involved in the second study, quoted by Quanta Magazine.
These investigations reinforce the idea that There are mathematical questions that will be forever unansweredhighlighting the limits of human knowledge.