
The gray tree by Piet Mondrian (1911)
A new research has discovered the mathematical principle that makes tree designs so easily recognizable, even in abstract works of art.
An innovator published in PNAS Nexus revealed that our ability to Recognize trees in works of art – Regardless of style or culture – is linked to a fundamental mathematical principle known as the scale exponent of the branches diameter.
This discovery suggests that even the abstract representations of trees maintain its recognizable form due to a Universal standard found in nature.
Held by researchers at the University of Michigan and the University of New Mexico, the study examined the way the thickness of trees branches influences our perception of their tree nature. The investigation is based on observations made by Artists like Leonardo da Vincibut applies a modern mathematical analysis to understand the phenomenon in greater depth.
“There are some art characteristics that are aesthetic or subjective, but we can use mathematics to describe them,” said main author Jingyi Gao.
His study focused on geometria fratala mathematical concept in which patterns are repeated at different scales. In trees, this manifests through branched structures that replicate in a self-syllable way.
The researchers specifically analyzed the scale exponent of the branches, which describes the way the thickness of the branches changes as the trees are divide into smaller sectionsrefers to.
Jingyi Gao e Mitchell Newberry
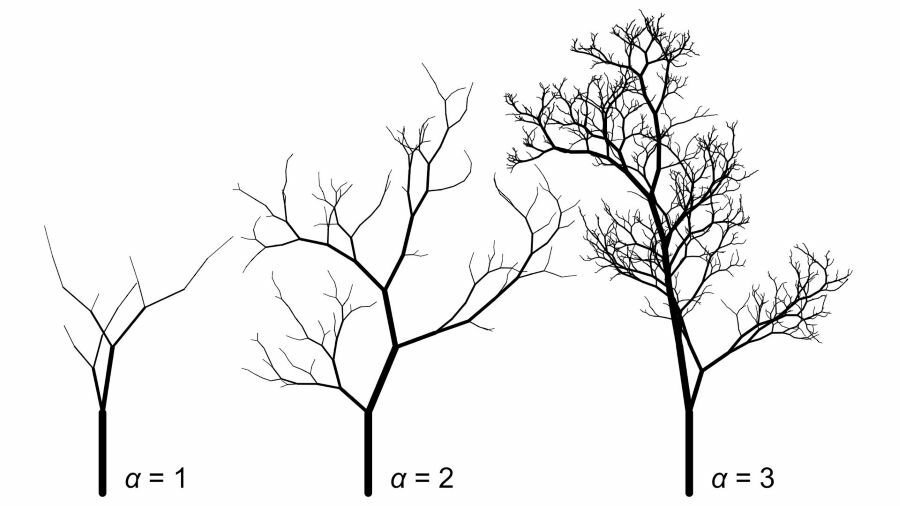
These computer -generated images show how the change in the scale exponent of the branch diameter – indicated by the Greek letter alpha – of a “tree” alters its appearance. Researchers showed that real trees and recognizable objects like trees in art have an alpha between 1.5 and 3.
In examining trees representations in various works of art – including sixteenth -century Indian stone sculptures, a Japanese eighteenth -century painting and Dutch modernist works from the early twentieth century – the team found that artists instinctively preserved this principle mathematical.
Even in highly stylized representations, trees maintained their recognizable form when the scale exponent corresponded to natural values, usually between 1.5 and 3.
A remarkable example is that of Dutch painter Piet Mondrian. In his 1911 work, The gray tree (The gray tree), Mondrian Used only black lines On a gray background, but the tree remained immediately recognizable. The researchers found that the scale exponent of the branches was within the break of the real trees.
However, in his later work of 1912, Flowering apple tree (Apple tree in flower), where the scale was changed, the tree became less distinguishablewith the designs opening the door to various interpretations, such as dancers, fish scales or abstract patterns.
The study highlights the way mathematical principles support artistic expression, reinforcing the idea that the structures inherent in nature shape human perception.


